Looking around for some data to play with, I stumbled-upon a small dataset that hopper is using as a teaser puzzle in their job posting for a data scientist. Taking a quick look in R…
options(scipen=999)
lapply(c("plyr","dplyr","ggplot2","scales","Hmisc","YaleToolkit","gpairs","RColorBrewer"),require,character.only=T,quietly=T)
system("cat ~/Downloads/puzzle.csv | (head -n 5 ; tail -n 5)")
0.3971497,2.1136286
0.3971497,2.1136286
0.3971497,2.1136286
0.3971497,2.1136286
0.3971497,2.1136286
0.6589491,-1.5535368
0.8439924,0.6126211
0.7515614,1.2998793
0.9068190,0.0774441
1.0608076,-2.8246059
hop <- read.csv("~/Downloads/puzzle.csv",header = F)
str(hop)
'data.frame': 1024 obs. of 2 variables:
$ V1: num 0.397 0.397 0.397 0.397 0.397 ...
$ V2: num 2.11 2.11 2.11 2.11 2.11 ...
sum(is.finite(hop$v1))
[1] 0
sum(is.finite(hop$v2))
[1] 0
summary(hop)
V1 V2
Min. :-0.9251 Min. :-2.8379
1st Qu.: 0.3930 1st Qu.:-1.5649
Median : 0.5914 Median :-1.1465
Mean : 0.5057 Mean :-0.3965
3rd Qu.: 0.7462 3rd Qu.: 0.5701
Max. : 1.2213 Max. : 3.0970
The dataset seems to be clean and straightforward. 1024 obs: Kilobyte? A few plots…
qplot(as.numeric(row.names(hop)),V1,data=hop,xlab = "Index")
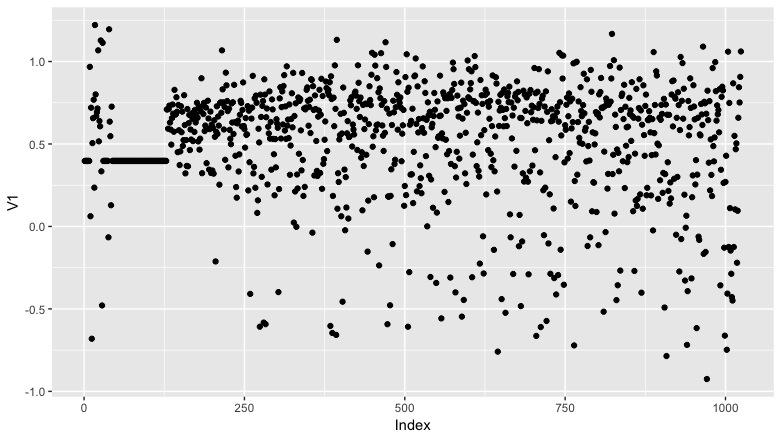
qplot(as.numeric(row.names(hop)),V2,data=hop,xlab = "Index")
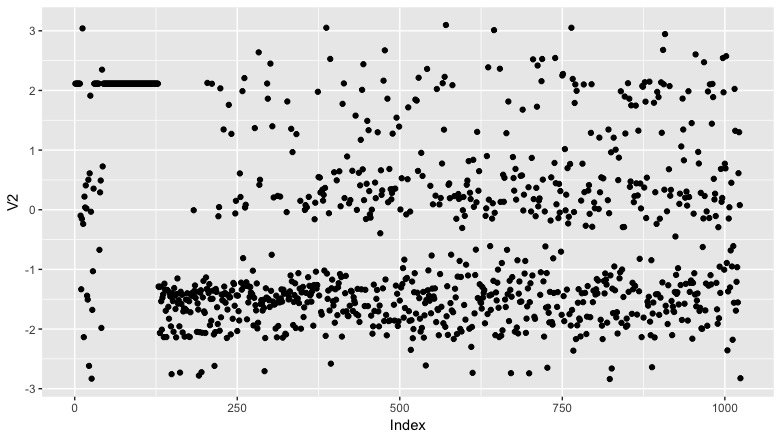
Patterns here. And weird groups of duplicates in both vars between index 0 and 125.
gpairs(hop)
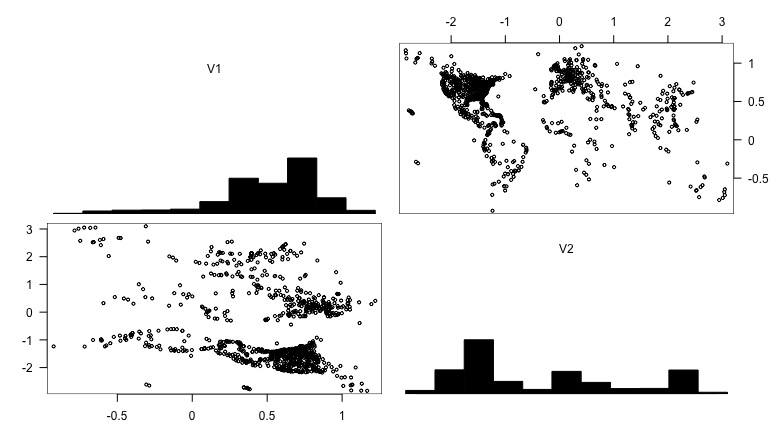
Looks like a world map!
with(hop,qplot(V2,V1))
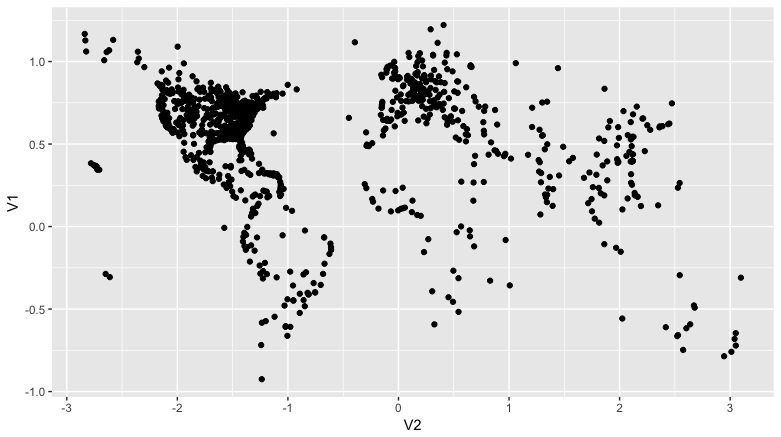
Clearly. Values of 1 on the Y axis appear to correspond to 60 degrees N/S latitude. Maybe all values have been divided by 60?
hop$lon <- hop$V2 * 60
hop$lat <- hop$V1 * 60
lapply(c("ggmap","maps","maptools","mapproj"),require,character.only=T,quietly=T)
basemap <- borders("world")
m <- ggplot() + basemap
m + geom_point(aes(x=hop$lon,y=hop$lat))
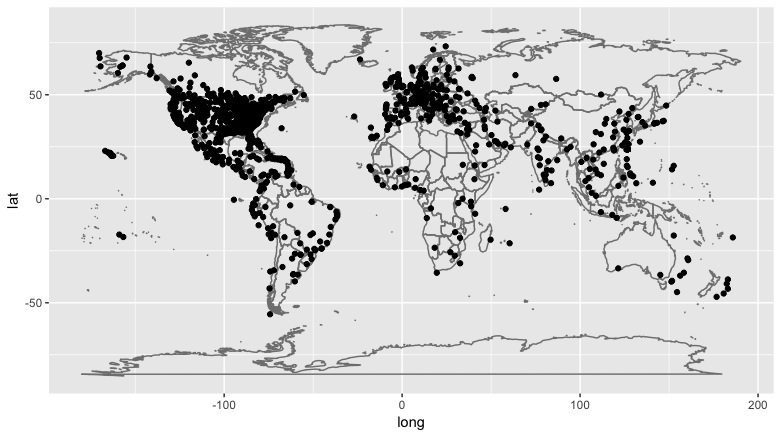
Not quite right. Easting goes beyond 180. Another projection? Looking at different options in Snyder’s manual I don’t think so. But I am reminded that formulas for working with projections are typically done in radians…
names(hop) <- c("v1","v2","lon60","lat60")
180/pi
[1] 57.29578
hop$lonrad2deg <- hop$v2 * 57.29578
hop$latrad2deg <- hop$v1 * 57.29578
m + geom_point(aes(x=hop$lonrad2deg,y=hop$latrad2deg))
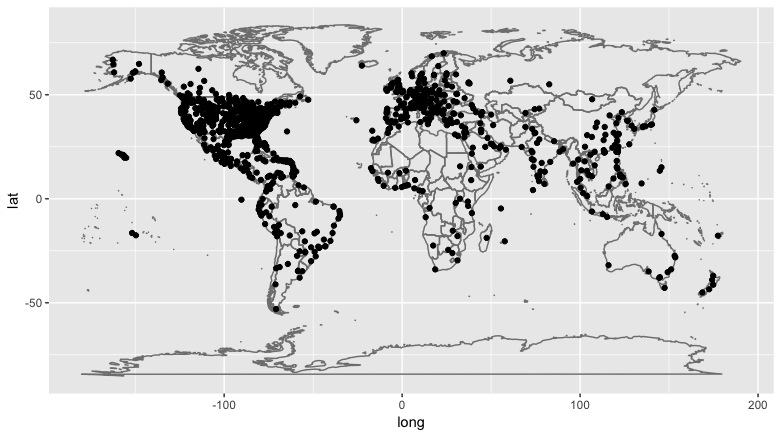
Nice! What about the duplicates?
coordsn <- count(hop,lon = lonrad2deg, lat = latrad2deg)
summary(coordsn)
lon lat n
Min. :-162.60 Min. :-53.00 Min. : 1.000
1st Qu.: -92.83 1st Qu.: 19.75 1st Qu.: 1.000
Median : -73.10 Median : 36.08 Median : 1.000
Mean : -37.97 Mean : 29.63 Mean : 1.119
3rd Qu.: 13.26 3rd Qu.: 43.46 3rd Qu.: 1.000
Max. : 177.44 Max. : 69.98 Max. :101.000
unique(coordsn$n)
[1] 1 2 101
dupset <- data.frame(subset(coordsn,n>1))
str(dupset)
'data.frame': 10 obs. of 3 variables:
$ lon: num -150 -122.4 -96.2 -86.3 -82.6 ...
$ lat: num 61.2 37.6 19.1 39.7 38.4 ...
$ n : int 2 2 2 2 2 2 2 2 2 101
dupset[dupset$n > 2,]
lon lat n
10 121.102 22.755 101
m + geom_point(aes(x=dupset$lon,y=dupset$lat))
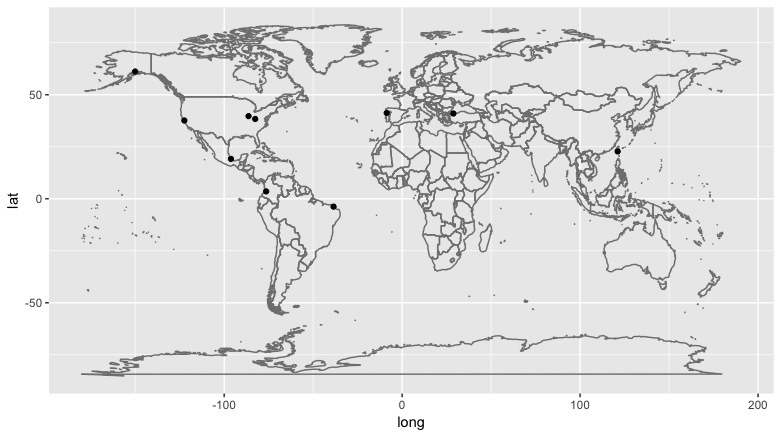
Weird. Seemingly no connection between locations with duplicates. Coming from hopper, I assume these are airports. I can plot points against OSM or similar basemap to confirm. But what is going on with the one in what looks like Taiwan with 101 of them? Maybe something like search traffic on hopper’s servers at a given moment. China’s population is so large that it’s possible.
Unfortunately, no more time for this right now. A future post…